椭球面是CAD、碰撞检测以及高维分子建模等领域的重要基础曲面。多维空间中的椭球拟合面临无法保证对输入数据的拟合结果一定是椭球面(ellipsoid-specific)、对大离心率椭球数据拟合误差大(unstable for large axis ratios)、对噪声和离群点敏感(sensitive to noise, outliers)以及拟合约束受限于数据嵌入的特定空间维度(dimension-dependent)等难题。

该工作从贝叶斯参数估计角度对多维空间的椭球拟合问题进行优化求解。不同与传统基于代数拟合或几何距离拟合的方式，该工作假设曲面上每点都可能是测量点的来源，将椭球拟合建模为贝叶斯后验估计过程，其中后验概率刻画了椭球面上每个点和测量点之间的对应关系。

该工作利用先验分布约束参数空间，保证拟合结果一定是椭球面，同时通过引入均匀分布刻画离群点，保证了算法对离群数据的强鲁棒性。该工作从KL散度角度证明了均匀分布对于算法鲁棒性的必要性，同时引入向量型机制对算法进一步加速优化。

该方法能同时解决多维空间椭球拟合所面临的所有难题，即保证拟合曲面一定是椭球面、不受大离心率椭球数据影响、对噪声和离群点具有强鲁棒性以及和数据嵌入的空间维度无关，同时给出了算法收敛性证明。该工作突破了传统椭球拟合算法的精度和鲁棒性，在生物显微细胞计数、CAD三维重建、几何形状逼近、地球磁力计矫正、高维空间及退化情形方面得到应用。

相关论文被人工智能领域顶级期刊IEEE Transactions on Pattern Analysis and Machine Intelligence（TPAMI, IF：24.314）接收发表。　

[1] Mingyang Zhao, Xiaohong Jia, Lei Ma, Yuke Shi, Jingen Jiang, Qizhai Li, Dong-Ming Yan, Tiejun Huang. A Bayesian Approach Toward Robust Multidimensional Ellipsoid-Specific Fitting，IEEE Transactions on Pattern Analysis and Machine Intelligence (T-PAMI), 10.1109/TPAMI.2024.3432913.

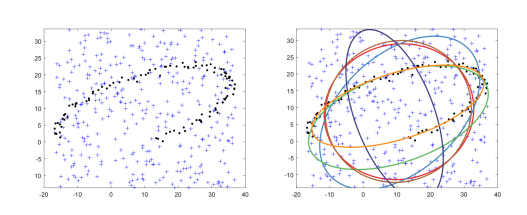
　　二维噪声和离群点干扰数据拟合结果对比(橘黄色代表本文方法)

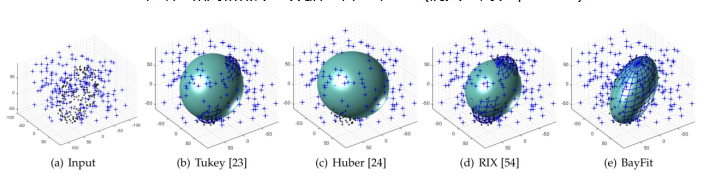
　　三维噪声和离群点干扰数据拟合结果对比(BayFit代表本文方法)

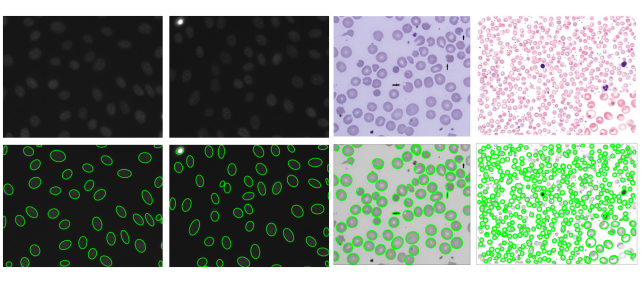
　　直接用于显微细胞和血细胞计数(未经任何后期优化)

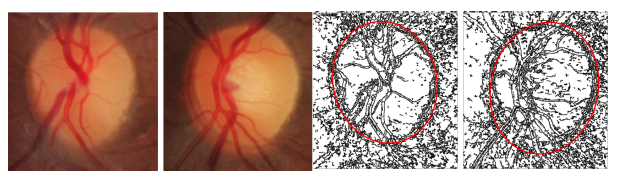
　　直接用于高噪声干扰下的视网膜识别(未经任何后期优化)

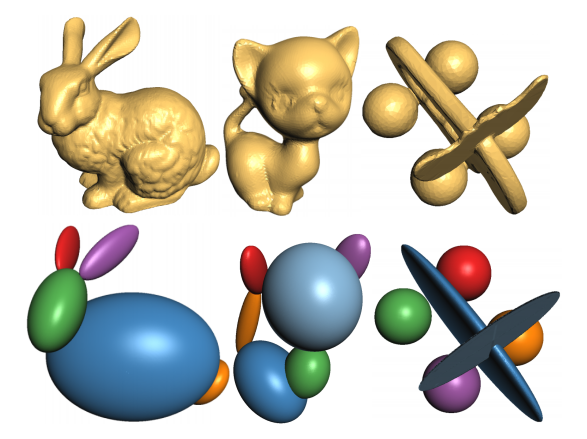
　　直接用于一般几何形状刻画